Menger Sponge
“In mathematics, the Menger sponge (also known as the Menger universal curve) is a fractal curve. It is a three-dimensional generalization of the Cantor set and Sierpinski carpet, though it is slightly different from a Sierpinski sponge. It was first described by Karl Menger in 1926, in his studies of the concept of topological dimension”
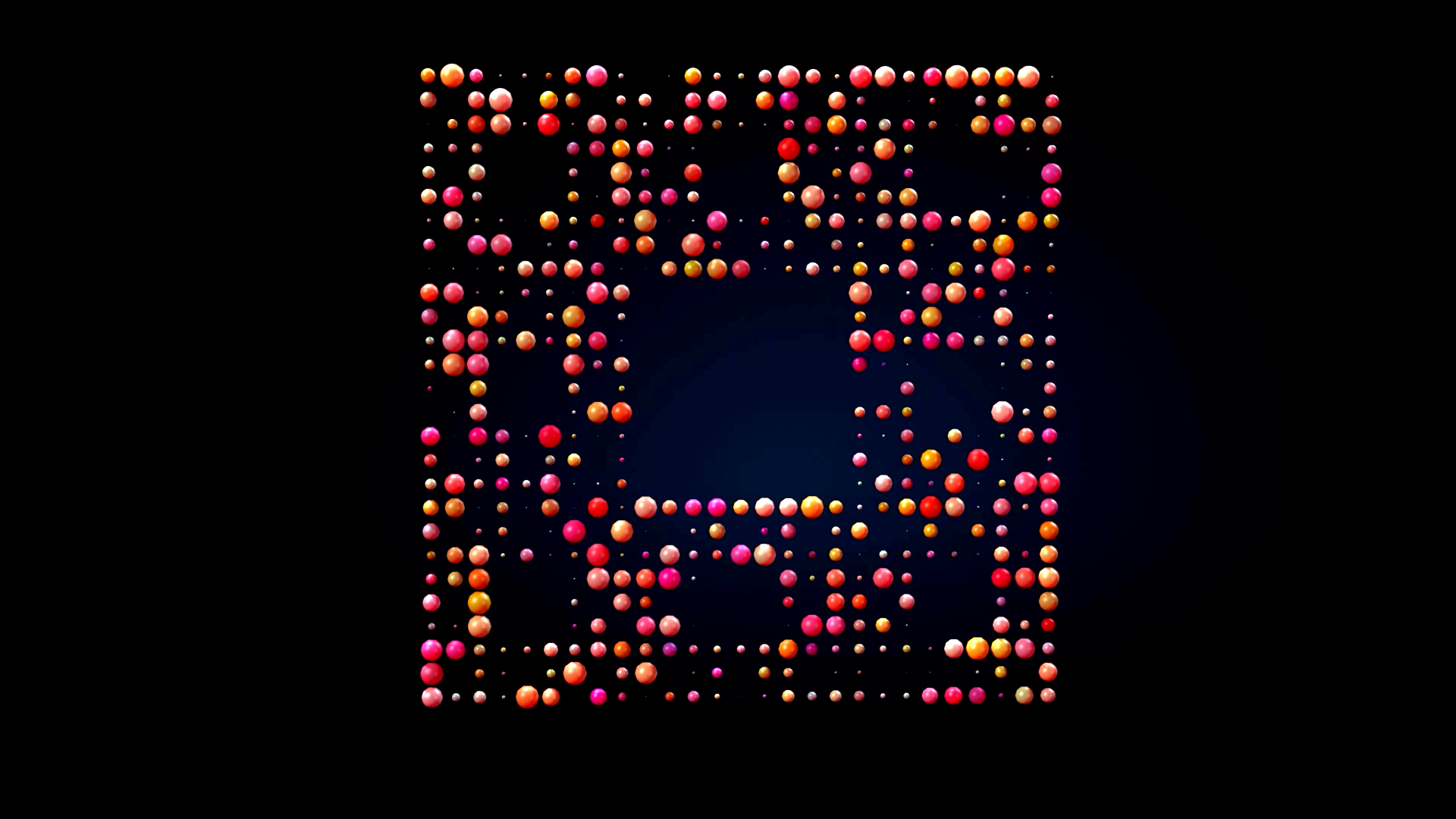
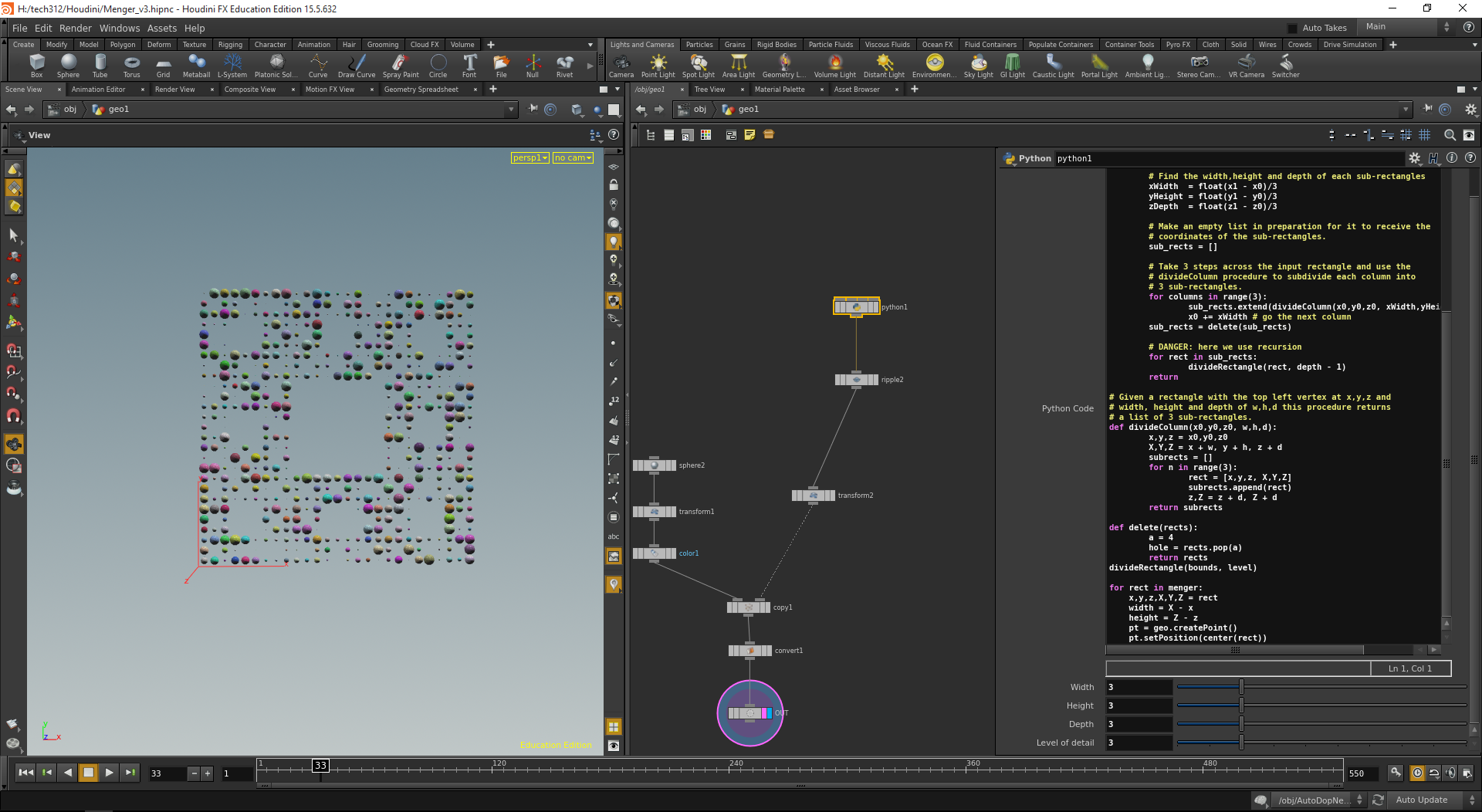
For this project I have tried to implement the provided Menger Sponge code in Houdini and had some fun with it, here is the result:
Breakdown:
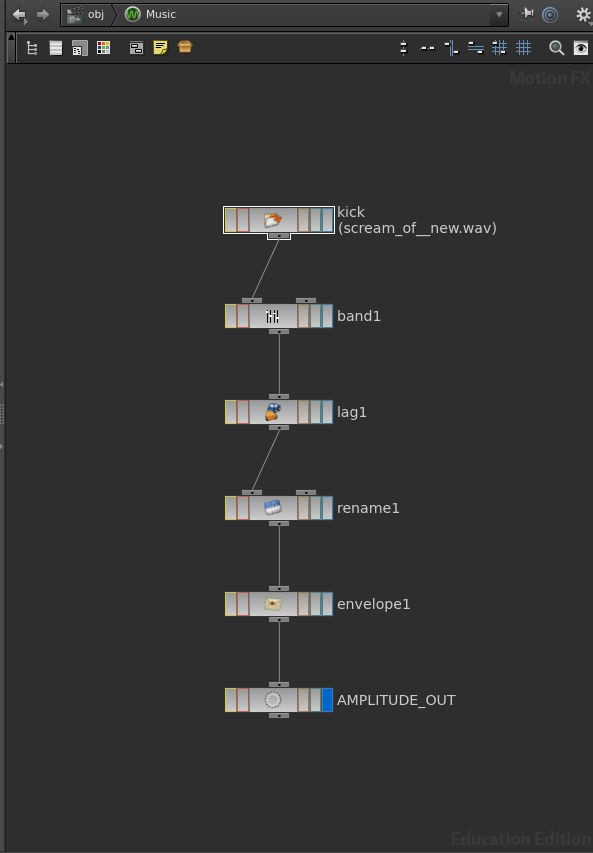
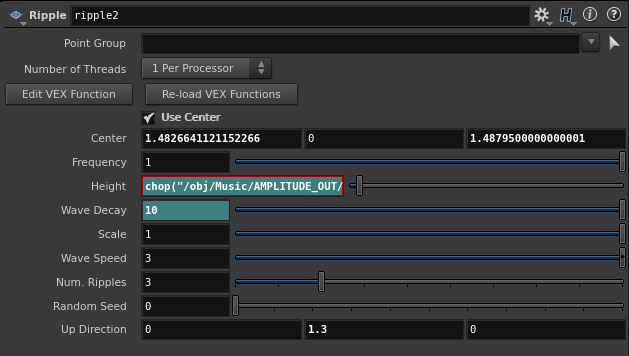
Then I used chops to Export the music wavelength and used it to animate my ripple on 2D Menger points
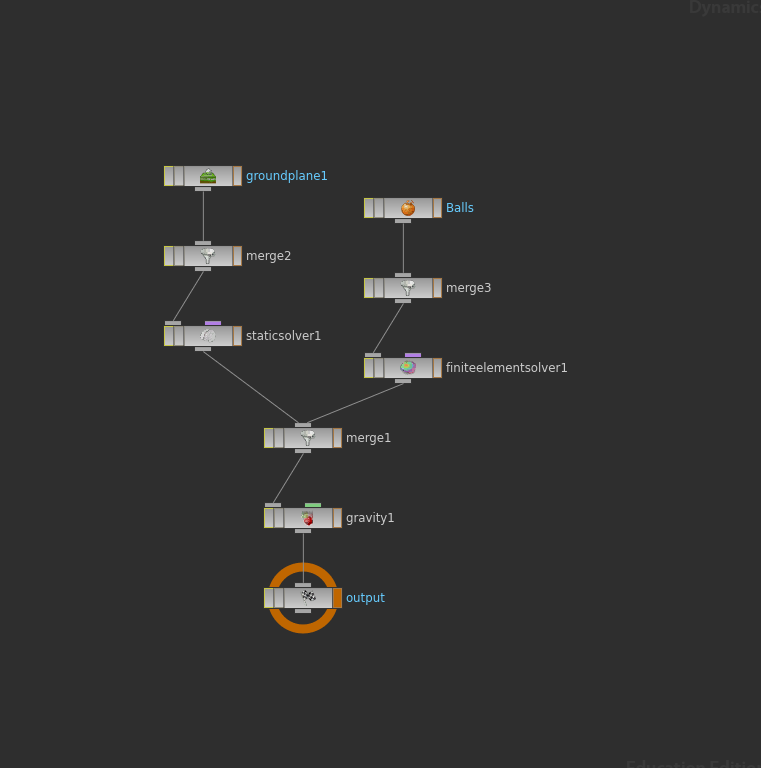
Finally I add soft body(FEM) to the whole animation
Here is the modified code for Houdini:
from random import uniform;
import random
menger = []
meng = hou.node(‘/obj/geo1/python1’)
boundx = float(meng.parm(“width”).eval())
boundy = float(meng.parm(“height”).eval())
boundz = float(meng.parm(“depth”).eval())
level = int(meng.parm(“level”).eval())
bounds = [0, 0, 0, boundx, boundy, boundz]
#midpoint of box
def center(bbox):
x,y,z,X,Y,Z = bbox
midpnt = []
midpnt = ((x+X)/2, (y+Y)/2, (z+Z)/2)
return midpnt
def divideRectangle(rect, depth):
if depth == 0:
menger.append(rect)
return
x0,y0,z0, x1,y1,z1 = rect
# Find the width,height and depth of each sub-rectangles
xWidth = float(x1 – x0)/3
yHeight = float(y1 – y0)/3
zDepth = float(z1 – z0)/3
# Make an empty list in preparation for it to receive the
# coordinates of the sub-rectangles.
sub_rects = []
# Take 3 steps across the input rectangle and use the
# divideColumn procedure to subdivide each column into
# 3 sub-rectangles.
for columns in range(3):
sub_rects.extend(divideColumn(x0,y0,z0, xWidth,yHeight,zDepth))
x0 += xWidth # go the next column
sub_rects = delete(sub_rects)
# DANGER: here we use recursion
for rect in sub_rects:
divideRectangle(rect, depth – 1)
return
# Given a rectangle with the top left vertex at x,y,z and
# width, height and depth of w,h,d this procedure returns
# a list of 3 sub-rectangles.
def divideColumn(x0,y0,z0, w,h,d):
x,y,z = x0,y0,z0
X,Y,Z = x + w, y + h, z + d
subrects = []
for n in range(3):
rect = [x,y,z, X,Y,Z]
subrects.append(rect)
z,Z = z + d, Z + d
return subrects
def delete(rects):
a = 4
hole = rects.pop(a)
return rects
divideRectangle(bounds, level)
for rect in menger:
x,y,z,X,Y,Z = rect
width = X – x
height = Z – z
pt = geo.createPoint()
pt.setPosition(center(rect))